Computational cosmology
Contents
1. Inflation with curvature
- paper arXiv
Recent analyses showed that a closed universe model can account for some features observed in the Planck satellite’s survey of the Cosmic Microwave Background (CMB). These features are not predicted by the “standard model of cosmology”, $\Lambda$CDM (where $\Lambda$ is the cosmological constant, and CDM stands for “cold dark matter”), which assumes spatial flatness. Adding a small positive curvature (leading to a slightly closed universe) can explain the observations better, which led to increased interest in these models.
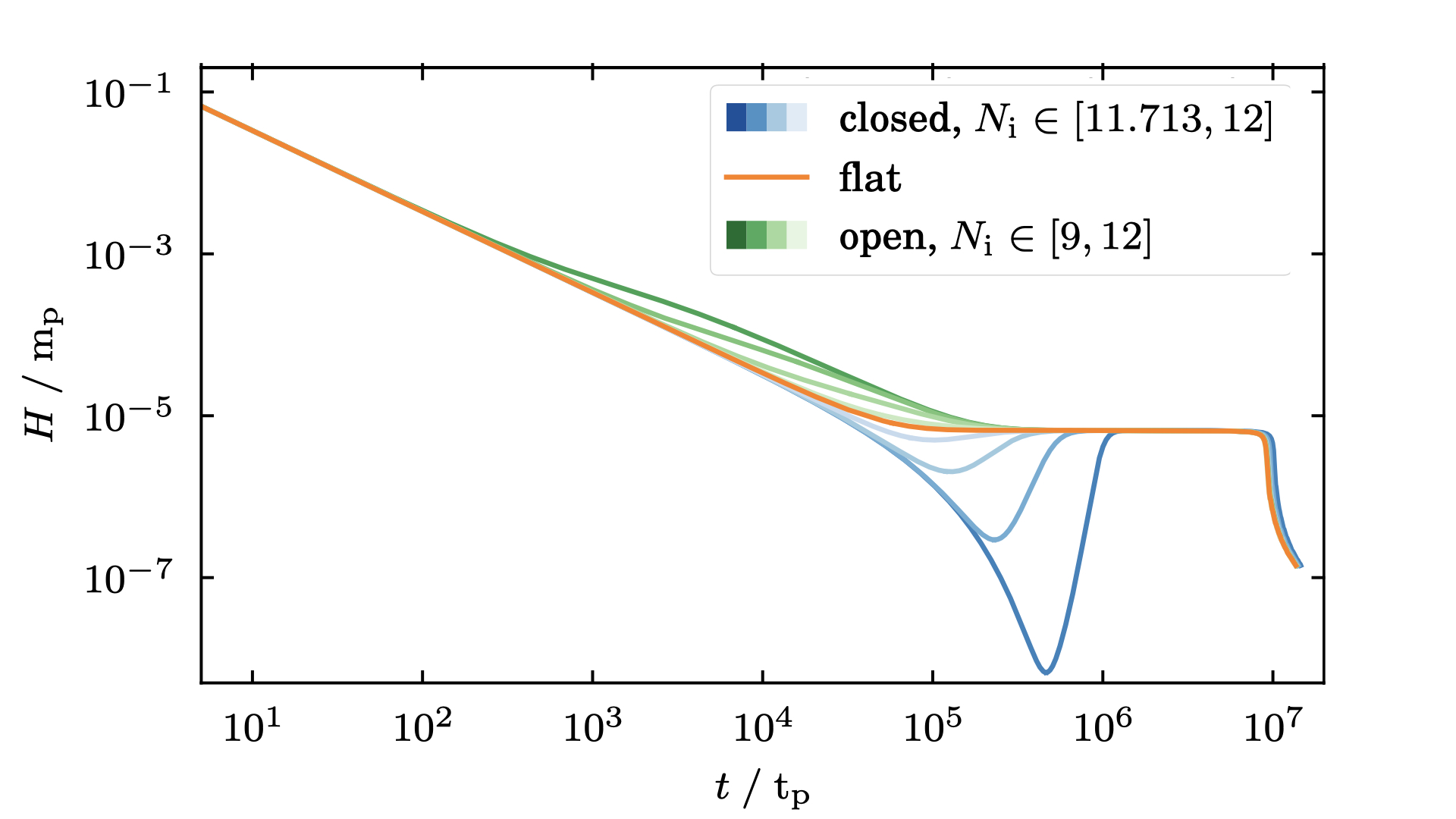
So far, closed universe studies have only considered the late-time effects of positive curvature, i.e. did not assume non-zero curvature from the start of the universe’s evolution. One reason behind this is the vast additional computational effort it would introduce. But even a small present-day curvature has serious implications for the universe’s past evoution. Positive curvature would significantly limit the amount of expansion the universe undergoes at early times (during cosmological inflation). Take a look at the evolution of the Hubble parameter (quantifies the rate of expansion) in open, c-osed, and flat universes (corresponding to negative, positive, and zero curvature, respectively):
This in turn leads to the breakdown of assumptions currently used about the distribution of perturbations in matter density at these times. All in all, this distribution (called the primordial power spectrum) would now need to be calculated numerically, and that involves the numerical solution of many, highly oscillatory ODEs. Here are some examples for primordial power spectra (left) and observable CMB temperature power spectra (right) in universes with different amounts of positive curvature:
and the same for negative curvature:
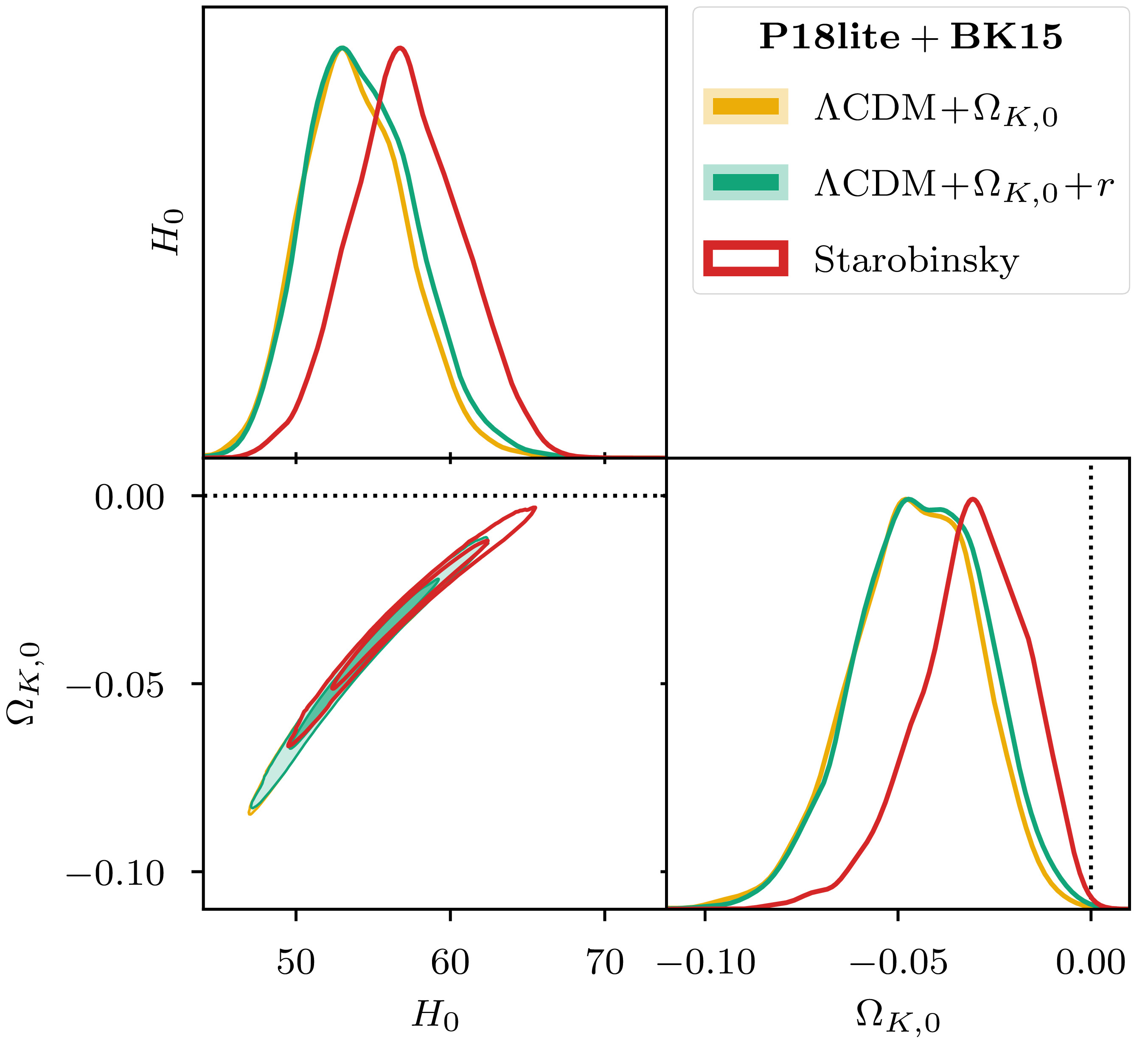
Thanks to its use of asymptotic expansions in the oscillatory regime, these problems are easy for oscode. We are thus able to numerically calculate the primordial power spectra of universes with various curvatures (see above :)), thus taking curvature into account from the start. This difference yields changes the posterior probability of parameters in the model. As an example, the posterior prediction for the present-day Hubble parameter $H_0$, and the present-day energy density in curvature, $\Omega_{K, 0}$ change like so:
where the $\Lambda CDM + \Omega_{K, 0} (+r)$ denote the standard $\Lambda CDM$ model augmented by a late-time curvature parameter, and “Starobinsky” is an inflationary model which allows for nonzero primordial curvature.